Pi
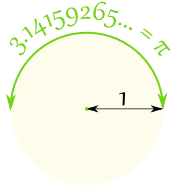 |
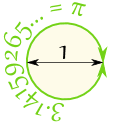
Draw a circle with a radius of 1. The distance half way around the edge of the circle will be 3.14159265... a number known as Pi |
| Or you could draw a circle with a diameter of 1. Then the circumference (the distance all the way around the edge of the circle) will be Pi |
 |
 |
Pi (the symbol is the Greek letter π) is:
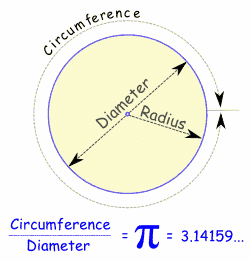
The ratio of the Circumference
to the Diameter of a Circle. |
| In other words, if you measure the circumference, and then divide by the diameter of the circle you get the number π It is approximately equal to:
3.14159265358979323846…
The digits go on and on with no pattern. In fact, π has been calculated to over one trillion decimal places and still there is no pattern. |
 |
Example: You walk around a circle which has a diameter of 100m, how far have you walked?
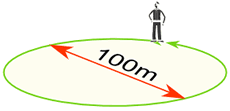 |
Distance walked = Circumference = π × 100m = 314.159...m
= 314m (to the nearest m)
|
Approximation
A quick and easy approximation for π is 22/7
22/7 = 3.1428571...
But as you can see, 22/7 is not exactly right. In fact π is not equal to the ratio of any two numbers, which makes it an irrational number.A better approximation (but stll not exact) is:
355/113 = 3.1415929...
(think "113355", then divide the "355" by the "113")
(think "113355", then divide the "355" by the "113")
Remembering
I usually just remember "3.14159", but you can also count the letters of:
"May I have a large container of butter today"
3 1 4 1 5 9 2 6 5
3 1 4 1 5 9 2 6 5
3.14159265358979323846264338327950288419716939937510 58209749445923078164062862089986280348253421170679...
e
 |
The number e is a famous irrational number, and is one of the most important numbers in mathematics. The first few digits are:
2.7182818284590452353602874713527 (and more ...)
It is often called Euler's number after Leonhard Euler |
e is found in many interesting areas, so it is worth learning about.
Calculating
There are many ways of calculating the value of e, but none of them ever give an exact answer, because e is irrational (not the ratio of two integers). But it is known to over 1 trillion digits of accuracy!For example, the value of (1 + 1/n)n approaches e as n gets bigger and bigger:
|
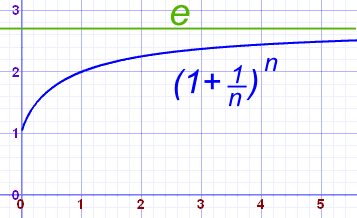 |
The value of e is also equal to 1 + 1/1! + 1/2! + 1/3! + 1/4! + 1/5! + 1/6! + 1/7! + ... (etc)
(Note: "!" means factorial)
The first few terms add up to: 1 + 1 + 1/2 + 1/6 + 1/24 + 1/120 = 2.718055556
Remembering
To remember the value of e (to 10 places) just remember this saying (count the letters!):- To
- express
- e
- remember
- to
- memorize
- a
- sentence
- to
- simplify
- this
2.7 1828 1828
And following THAT is the angles in a Right-Angled Isosceles (two equal angles) Triangle of 45°, 90°, 45°:
2.7 1828 1828 45 90 45
Golden Ratio
 |
The golden ratio (symbol is the Greek letter "phi" shown at left) is a special number approximately equal to 1.618 It appears many times in geometry, art, architecture and other areas. |
The Idea Behind It
If you divide a line into two parts so that:
|
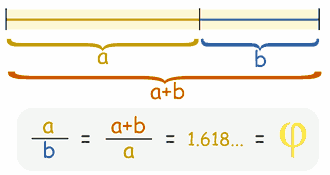 |
Beauty
 |
This rectangle has been made using the Golden Ratio, Looks like a typical frame for a painting, doesn't it? Some artists and architects believe the Golden Ratio makes the most pleasing and beautiful shape. |
Do you think it is the "most pleasing rectangle"?
Maybe you do or don't, that is up to you!
| Many buildings and artworks have the Golden Ratio in them, such as the Parthenon in Greece, but it is not really known if it was designed that way. |
 |
The Actual Value
The Golden Ratio is equal to:
1.61803398874989484820... (etc.)
The digits just keep on going, with no pattern. In fact the Golden Ratio is known to be an Irrational Number, and I will tell you more about it later.Calculating It
You can calculate it yourself by starting with any number and following these steps:- A) divide 1 by your number (=1/number)
- B) add 1
- C) that is your new number, start again at A
| Number | 1/Number | Add 1 |
|---|---|---|
| 2 | 1/2=0.5 | 0.5+1=1.5 |
| 1.5 | 1/1.5 = 0.666... | 0.666... + 1 = 1.666... |
| 1.666... | 1/1.666... = 0.6 | 0.6 + 1 = 1.6 |
| 1.6 | 1/1.6 = 0.625 | 0.625 + 1 = 1.625 |
| 1.625 | 1/1.625 = 0.6154... | 0.6154... + 1 = 1.6154... |
| 1.6154... |
But it takes a long time to get even close, however there are better ways and it can be calculated to thousands of decimal places quite quickly.
Drawing It
Here is one way to draw a rectangle with the Golden Ratio:
|
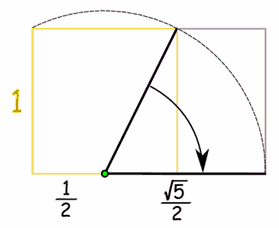 |
The Formula
Looking at the rectangle we just drew, you can see that there is a simple formula for it. If one side is 1, the other side will be:Fibonacci Sequence
There is a special relationship between the Golden Ratio and the Fibonacci Sequence:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...
(The next number is found by adding up the two numbers before it.)
And here is a surprise: if you take any two successive (one after the other) Fibonacci Numbers, their ratio is very close to the Golden Ratio. In fact, the bigger the pair of Fibonacci Numbers, the closer the approximation. Let us try a few:
A
|
B
|
B/A | |
|---|---|---|---|
2
|
3
|
1.5 | |
3
|
5
|
1.666666666... | |
5
|
8
|
1.6 | |
8
|
13
|
1.625 | |
...
|
...
|
... | |
144
|
233
|
1.618055556... | |
233
|
377
|
1.618025751... | |
...
|
...
|
... |
A
|
B
|
B / A
|
|
|---|---|---|---|
192
|
16
|
0.08333333... | |
16
|
208
|
13 | |
208
|
224
|
1.07692308... | |
224
|
432
|
1.92857143... | |
...
|
...
|
... | |
7408
|
11984
|
1.61771058... | |
11984
|
19392
|
1.61815754... | |
...
|
...
|
... |
The Most Irrational ...
I believe the Golden Ratio is the most irrational number. Here is why ...| One of the special properties of the Golden Ratio is that it can be defined in terms of itself, like this: | |
| (In numbers: 1.61803... = 1 + 1/1.61803...) | |
| That can be expanded into this fraction that goes on for ever (called a "continued fraction"): | |
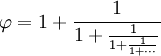 |
|
So, it neatly slips in between simple fractions.
Whereas many other irrational numbers are reasonably close to
rational numbers (for example Pi = 3.141592654... is pretty close to
22/7 = 3.1428571...)Other Names
The Golden Ratio is also sometimes called the golden section, golden mean, golden number, divine proportion, divine section and golden proportion.Feigenbaum Constant
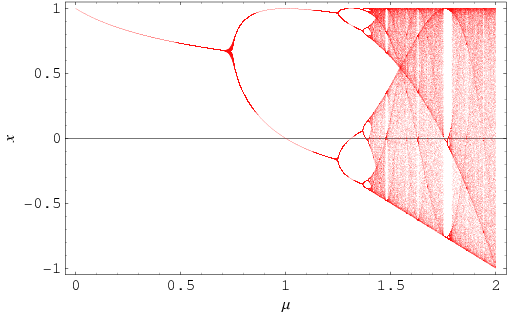
The Feigenbaum constant 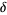 is a universal
constant for functions approaching chaos via period
doubling. It was discovered by Feigenbaum in 1975 (Feigenbaum 1979) while studying
the fixed points of the iterated function
is a universal
constant for functions approaching chaos via period
doubling. It was discovered by Feigenbaum in 1975 (Feigenbaum 1979) while studying
the fixed points of the iterated function
and characterizes the geometric approach of the bifurcation parameter to its limiting value as the parameter 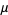 is increased for
fixed
is increased for
fixed  . The plot above is made by iterating
equation (1) with
. The plot above is made by iterating
equation (1) with 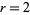 several hundred
times for a series of discrete but closely spaced values of
several hundred
times for a series of discrete but closely spaced values of 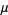 , discarding the
first hundred or so points before the iteration has settled down to its fixed points,
and then plotting the points remaining.
, discarding the
first hundred or so points before the iteration has settled down to its fixed points,
and then plotting the points remaining.
 A similar plot that more directly shows the cycle may be constructed by plotting
A similar plot that more directly shows the cycle may be constructed by plotting 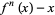 as a function of
as a function of 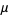 . The plot above
(Trott, pers. comm.) shows the resulting curves for
. The plot above
(Trott, pers. comm.) shows the resulting curves for 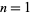 , 2, and 4.
, 2, and 4.
Let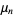 be the point at which a period
be the point at which a period 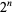 -cycle appears, and denote the converged value
by
-cycle appears, and denote the converged value
by 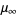 . Assuming geometric convergence,
the difference between this value and
. Assuming geometric convergence,
the difference between this value and 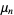 is denoted
is denoted
where 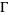 is a constant and
is a constant and 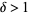 is a
constant now known as the Feigenbaum constant. Solving for
is a
constant now known as the Feigenbaum constant. Solving for 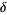 gives
gives
(Rasband 1990, p. 23; Briggs 1991). An additional constant 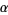 , defined as
the separation of adjacent elements of period doubled attractors from one double to the next, has a value
, defined as
the separation of adjacent elements of period doubled attractors from one double to the next, has a value
where 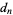 is the value of the nearest cycle
element to 0 in the
is the value of the nearest cycle
element to 0 in the 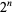 cycle (Rasband
1990, p. 37; Briggs 1991).
cycle (Rasband
1990, p. 37; Briggs 1991).
For equation (1) with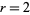 , the onsets
of bifurcations occur at
, the onsets
of bifurcations occur at 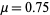 , 1.25, 1.368099,
1.39405, 1.399631, ..., giving convergents to
, 1.25, 1.368099,
1.39405, 1.399631, ..., giving convergents to 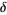 for
for 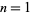 , 2, 3, ... of
4.23374, 4.5515, 4.64617, ....
, 2, 3, ... of
4.23374, 4.5515, 4.64617, ....
For the logistic map,
(Sloane's A006890, A098587, and A006891; Broadhurst 1999; Wolfram 2002,
p. 920),
where 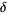 is known as the Feigenbaum constant
and
is known as the Feigenbaum constant
and 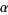 is the associated "reduction
parameter."
is the associated "reduction
parameter."
Briggs (1991) calculated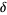 to 84 digits,
Briggs (1997) to 576 decimal places (of which 344 were correct), and Broadhurst (1999)
to 1018 decimal places. It is not known if the Feigenbaum constant
to 84 digits,
Briggs (1997) to 576 decimal places (of which 344 were correct), and Broadhurst (1999)
to 1018 decimal places. It is not known if the Feigenbaum constant 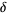 is algebraic,
or if it can be expressed in terms of other mathematical constants (Borwein and Bailey
2003, p. 53).
is algebraic,
or if it can be expressed in terms of other mathematical constants (Borwein and Bailey
2003, p. 53).
Briggs (1991) calculated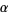 to 107 digits,
Briggs (1997) to 576 decimal places (of which 346 were correct), and Broadhurst (1999)
to 1018 decimal places.
to 107 digits,
Briggs (1997) to 576 decimal places (of which 346 were correct), and Broadhurst (1999)
to 1018 decimal places.
Amazingly, the Feigenbaum constant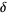 and associated
reduction parameter
and associated
reduction parameter 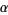 are "universal"
for all one-dimensional maps
are "universal"
for all one-dimensional maps 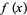 if
if 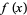 has a single
locally quadratic maximum. This was conjecture by Feigenbaum,
and demonstrated rigorously by Lanford (1982) for the case
has a single
locally quadratic maximum. This was conjecture by Feigenbaum,
and demonstrated rigorously by Lanford (1982) for the case 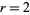 , and by Epstein
(1985) for all
, and by Epstein
(1985) for all 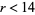 .
.
More specifically, the Feigenbaum constant is universal for one-dimensional maps if the Schwarzian derivative
is negative in the bounded interval (Tabor 1989, p. 220). Examples of maps which are universal include the Hénon
map, logistic map, Lorenz
attractor, Navier-Stokes truncations, and sine map 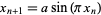 .
The value of the Feigenbaum constant can be computed explicitly using functional
group renormalization theory. The universal constant also occurs in phase transitions
in physics.
.
The value of the Feigenbaum constant can be computed explicitly using functional
group renormalization theory. The universal constant also occurs in phase transitions
in physics.
The value of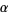 for a universal map may be approximated
from functional group renormalization theory to the zeroth order by solving
for a universal map may be approximated
from functional group renormalization theory to the zeroth order by solving
which can be rewritten as the quintic equation
Solving numerically for the smallest real root gives 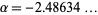 ,
only 0.7% off from the actual value (Feigenbaum 1988).
,
only 0.7% off from the actual value (Feigenbaum 1988).
For an area-preserving two-dimensional map with
the Feigenbaum constant is 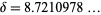 (Tabor 1989, p. 225).
(Tabor 1989, p. 225).
For a function of the form (1), the Feigenbaum constant for various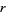 is given in the following table (Briggs
1991, Briggs et al. 1991, Finch 2003), which updates the values in Tabor (1989,
p. 225).
is given in the following table (Briggs
1991, Briggs et al. 1991, Finch 2003), which updates the values in Tabor (1989,
p. 225).
Broadhurst (1999) considered additional Feigenbaum constants. Let 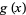 and
and 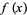 be even functions
with
be even functions
with 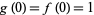 and
and
and 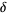 as large as possible. Let
as large as possible. Let 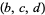 be positive
numbers with
be positive
numbers with
and 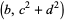 as small as possible. Also
let
as small as possible. Also
let 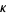 be the order of the nearest singularity,
with
be the order of the nearest singularity,
with
as 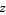 tends to zero. The values of these constants
are summarized in the following table.
tends to zero. The values of these constants
are summarized in the following table.
|
(1)
|
 A similar plot that more directly shows the cycle may be constructed by plotting
A similar plot that more directly shows the cycle may be constructed by plotting Let
|
(2)
|
|
(3)
|
|
(4)
|
For equation (1) with
For the logistic map,
|
(5)
| |||
|
(6)
| |||
|
(7)
| |||
|
(8)
|
Briggs (1991) calculated
Briggs (1991) calculated
Amazingly, the Feigenbaum constant
More specifically, the Feigenbaum constant is universal for one-dimensional maps if the Schwarzian derivative
|
(9)
|
The value of
|
(10)
|
|
(11)
|
For an area-preserving two-dimensional map with
|
(12)
| |||
|
(13)
|
For a function of the form (1), the Feigenbaum constant for various
| | | |
| 3 | 5.9679687038... | 1.9276909638... |
| 4 | 7.2846862171... | 1.6903029714... |
| 5 | 8.3494991320... | 1.5557712501... |
| 6 | 9.2962468327... | 1.4677424503... |
|
(14)
| |||
|
(15)
|
|
(16)
|
|
(17)
|
| constant | Sloane | value |
| A119277 | 0.83236723690531642484... | |
| A119278 | 1.8312589849371314853... | |
| A119279 | 2.6831509004740718014... | |
| A119280 | 1.3554618047064087438... |
No comments:
Post a Comment